Der 5. Tag des Astronomie-Kurses fand wieder in der Schule statt. Für die Außenbeobachtung am Astroplatz war das Wetter wegen der dichten Wolken ungeeignet; außerdem stand die Vollmondphase bevor und bei aufgehelltem Himmel kann man leider nicht viel DeepSky-Objekte erkennen.
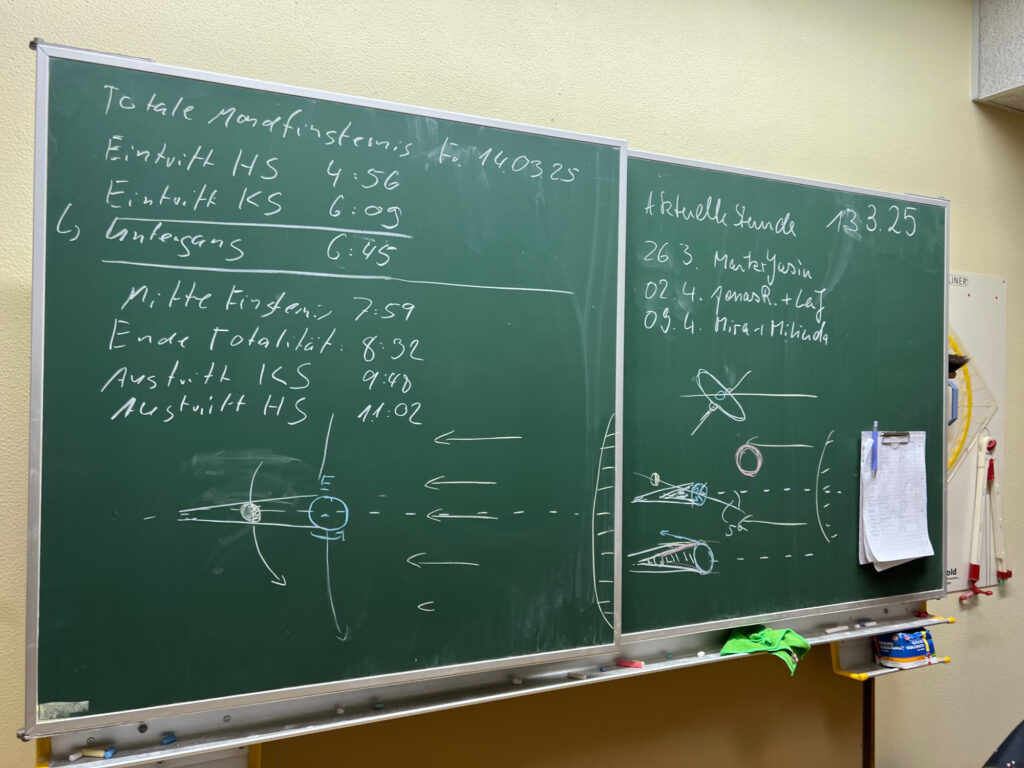
Wir begannen den Kurstag mit einem Ereignis, welches am Ende der Woche, nämlich am Freitag, den 14. März unmittelbar bevorstand: Eine totale Mondfinsternis. Zunächst wurde anhand von Tafelzeichnungen erklärt, unter welchen Umständen eine totale Mondfinsternis stattfindet. Denn es reicht nämlich nicht, dass Mond, Erde und Sonne in einer Reihe stehen (die typische Vollmondphase), sondern der Mond muss, um in den Kernschatten der Erde zu gelangen, sich in der Nähe der Ekliptikebene (der Umlaufebene der Erde um die Sonne) befinden.
Da jedoch die Mondbahn gegenüber dieser Ebene um ca. 5° geneigt ist, kann das nur passieren, wenn der Mond sich in der Nähe der auf- oder absteigenden Knoten befindet. Diese Punkte sind durch die sogenannte Knotenlinie verbunden. Sie ist die Schnittlinie zwischen der Ekliptikebene und der Umlaufebene der um 5° geneigten Mondbahn um die Erde.
Um zweiten Teil des Kurses wurde es dann richtig mathematisch:
Zunächst wurden neben den Winkeleinheiten (Grad und Radiant) wurden auch Einheiten kleinerer Winkel besprochen, etwa die Winkelminute als 60. Teil eines Grades und die Winkelsekunde als 3600er Teil einer Grades.
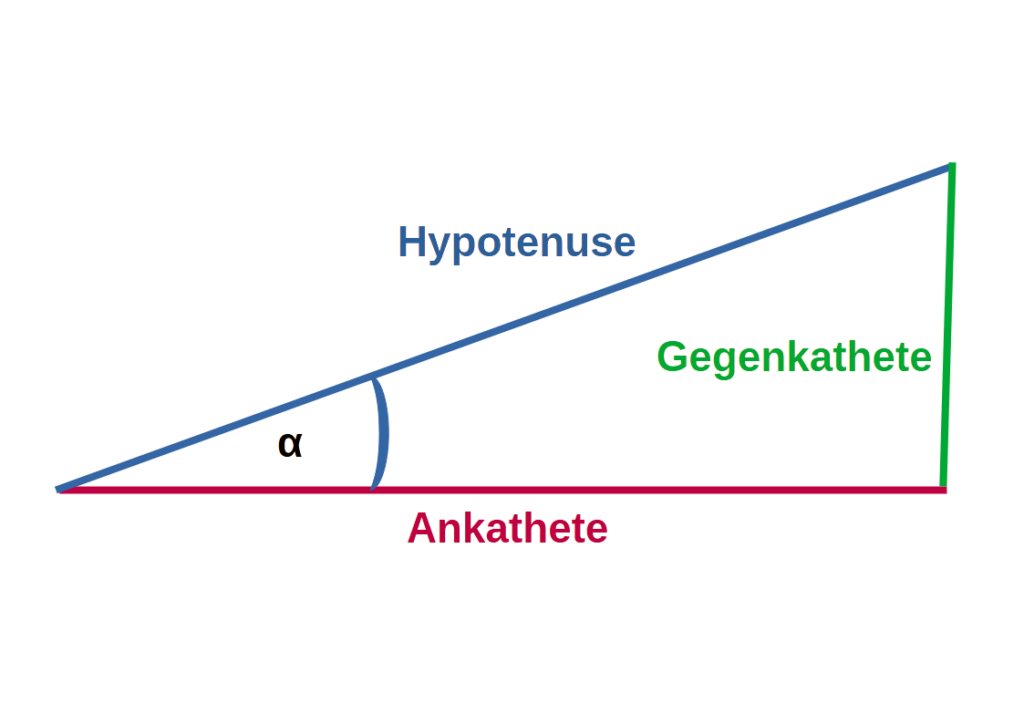
Danach ging um die Winkelwissenschaft – die Trigonometrie. Insbesondere um Winkel, die in rechtwinkligen Dreiecken auftreten. Denn mit Hilfe von rechtwinkligen Dreiecken lassen sich sehr viele grundsätzliche astronomische Sachverhalte berechnen, z.B. Entfernungen, Winkelausdehnungen, Parallaxen (Definition des Parsec), optische Strahlenverläufe in Teleskopen u.v.m. Hierbei spielen die sog. trigonometrischen Funktionen eine entscheidenden Rolle:
Sinus sin(α) = Gegenkathete / Hypotenuse
Cosinus cos(α) = Ankathete / Hypotenuse
und
Tangens tan(α) = Gegenkathete / Ankathete
Als Beispiel wurde die Winkelausdehnung des Vollmondes berechnet; also die Größe, die der Mond am Himmel einnimmt. Bei einer Durchschnittsentfernung von ca. 384000 km und einem Mondradius von ca. 1735 km kamen wir auf einen Winkel von
αMond = 2*arctan(1735 / 384000) = 31.1′ (Winkelminuten)
Als ‚Hausaufgabe‘ wurde die Berechnung der Winkelausdehnung der Sonne aufgegeben; mal sehen, ob jemandem was auffällt!
Aber auch die (theoretische) Winkelausdehnung des Sterns Beteigeuze wurde mit Hilfe des Tangens zwischen seiner geschätzten Größe (700-facher Sonnenradius) und seiner geschätzten Entfernung (550 Lichtjahre) ermittelt. Das eigentliche Problem war dabei, dass man die Größen des Quotienten
Sternradius / Entfernung in gleichen Einheiten, also in Kilometern, umrechnen musste…
Wir errechneten übrigens einen Winkel von 38.6mas (Milli-Winkelsekunden) für den scheinbaren Öffnungswinkel von Beteigeuze.